We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We investigate subgroups of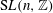 
$\text{SL}(n,\mathbb{Z})$ which preserve an open nondegenerate convex cone in 
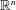$\mathbb{R}^{n}$ and admit in that cone as fundamental domain a polyhedral cone of which some faces are allowed to lie on the boundary. Examples are arithmetic groups acting on self-dual cones, Weyl groups of certain Kac–Moody algebras, and they do occur in algebraic geometry as the automorphism groups of projective manifolds acting on their ample cones.
