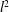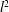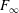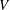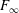Acyclic groups of low dimension are considered. To indicate the results simply, let $G^{\prime}$ be the nontrivial perfect commutator subgroup of a finitely presentable group $G$. Then $\mathrm{def}(G)\leq1$. When $\mathrm{def}(G)=1$, $G^{\prime}$ is acyclic provided that it has no integral homology in dimensions above 2 (a sufficient condition for this is that $G^{\prime}$ be finitely generated); moreover, $G/G^{\prime}$ is then $Z$ or $Z^{2}$. Natural examples are the groups of knots and links with Alexander polynomial 1. A further construction is given, based on knots in $S^{2}\times S^{1}$. In these geometric examples, $G^{\prime}$ cannot be finitely generated; in general, it cannot be finitely presentable. When $G$ is a 3-manifold group it fails to be acyclic; on the other hand, if $G^{\prime}$ is finitely generated it has finite index in the group of a $\mathbb{Q}$-homology 3-sphere.
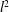 ${l}^{2}$-invisibility and a class of local similarity groups
${l}^{2}$-invisibility and a class of local similarity groups