We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It is known that if f is a real valued function on a rational vector space V, δ > 0,
1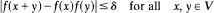
and if f is unbounded then f(x + y) = f(x)f(y) for all x, y ∊ V. In response to a problem of E. Lukacs, in this paper we study the bounded solutions of (1). For example, it is shown that if f is a bounded solution of (1) then - δ ≤ f(x) ≤ (1 + (1 + 4δ)1/2)/2 for all x ∊ V and these bounds are optimal.
