Given two unital C*-algebras equipped with states and a positive operator in the enveloping von Neumann algebra of their minimal tensor product, we define three parameters that measure the capacity of the operator to align with a coupling of the two given states. Further, we establish a duality formula that shows the equality of two of the parameters for operators in the minimal tensor product of the relevant C*-algebras. In the context of abelian C*-algebras, our parameters are related to quantitative versions of Arveson's null set theorem and to dualities considered in the theory of optimal transport. On the other hand, restricting to matrix algebras we recover and generalize quantum versions of Strassen's theorem. We show that in the latter case our parameters can detect maximal entanglement and separability.

Based on the Gale–Ryser theorem [2, 6], for the existence of suitable 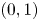$(0,1)$-matrices for different partitions of a natural number, we revisit the classical result of Lorentz [4] regarding the characterization of a plane measurable set, in terms of its cross-sections, and extend it to general measure spaces.

We extend results proved by the second author (Amer. J. Math., 2009) for nonnegatively curved Alexandrov spaces to general compact Alexandrov spaces $X$ with curvature bounded below. The gradient flow of a geodesically convex functional on the quadratic Wasserstein space $\left( \mathcal{P}\left( X \right),\,{{W}_{2}} \right)$ satisfies the evolution variational inequality. Moreover, the gradient flow enjoys uniqueness and contractivity. These results are obtained by proving a first variation formula for the Wasserstein distance.

A notion of entropy for the non-singular action of finite co-ordinate changes on is introduced. This quantity-average co-ordinate or AC entropy-is calculated for product measures and G-measures. It is shown that the type III classes can be subdivided using AC entropy. An equivalence relation is established for which AC entropy is an invariant.

An F-measure on a Cartesian product of algebras of sets is a scalar-valued function which is a scalar measure independently in each coordinate. It is demonstrated that an F-measure on a product of algebras determines an F-measure on the product of the corresponding σ-algebras if and only if its Fréchet variation is finite. An analogous statement is obtained in a framework of fractional Cartesian products of algebras, and a measurement of p-variation of F-measures, based on Littlewood-type inequalities, is discussed.

We give a simple proof that, for any ॉ > 0, there is an outer measure μ* on a finite set X such that, for any measure Thus there is a non-zero outer (finitely subadditive) measure v* on the clopen subsets of the Cantor set such that, if v ≤ v* is a finitely additive measure on the clopen subsets of the Cantor set, then v ≡ 0.

A general procedure is introduced for identifying categories of Cauchy spaces which have completions which possess a certain convergence property P, and for constructing completion functors on such categories. These results are applied to obtain a characterization of Cauchy spaces which allow T3 completions, and to construct T3 completions for categories of Cauchy groups and Cauchy lattices.