In this paper, we first prove that for 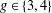 $g\in \{3,4\}$, there are infinitely many 3-geodesic transitive but not 3-arc transitive graphs of girth
$g\in \{3,4\}$, there are infinitely many 3-geodesic transitive but not 3-arc transitive graphs of girth 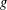 $g$ with arbitrarily large diameter and valency. Then we classify the family of 3-geodesic transitive but not 3-arc transitive graphs of valency 3 and those of valency 4 and girth 4.
$g$ with arbitrarily large diameter and valency. Then we classify the family of 3-geodesic transitive but not 3-arc transitive graphs of valency 3 and those of valency 4 and girth 4.