Let 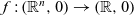 $f\,{:}\,(\mathbb R^n,0)\to (\mathbb R,0)$
be an analytic function germ with non-isolated singularities and let
$f\,{:}\,(\mathbb R^n,0)\to (\mathbb R,0)$
be an analytic function germ with non-isolated singularities and let 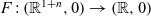 $F\,{:}\, (\mathbb{R}^{1+n},0) \to (\mathbb{R},0)$
be a 1-parameter deformation of f. Let
$F\,{:}\, (\mathbb{R}^{1+n},0) \to (\mathbb{R},0)$
be a 1-parameter deformation of f. Let 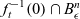 $ f_t ^{-1}(0) \cap B_\epsilon^n$
,
$ f_t ^{-1}(0) \cap B_\epsilon^n$
, 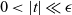 $0 < \vert t \vert \ll \epsilon$
, be the “generalized” Milnor fiber of the deformation F. Under some conditions on F, we give a topological degree formula for the Euler characteristic of this fiber. This generalizes a result of Fukui.
$0 < \vert t \vert \ll \epsilon$
, be the “generalized” Milnor fiber of the deformation F. Under some conditions on F, we give a topological degree formula for the Euler characteristic of this fiber. This generalizes a result of Fukui.