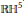1 results
On the Geometry of the Moduli Space of Real Binary Octics
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 4 / 01 August 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 755-797
- Print publication:
- 01 August 2011
-
- Article
-
- You have access
- Export citation
-
The moduli space of smooth real binary octics has five connected components. They parametrize the real binary octics whose defining equations have 0, … , 4 complex-conjugate pairs of roots respectively. We show that each of these five components has a real hyperbolic structure in the sense that each is isomorphic as a real-analytic manifold to the quotient of an open dense subset of 5-dimensional real hyperbolic space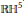
$\mathbb{R}{{\mathbb{H}}^{5}}$ by the action of an arithmetic subgroup of Isom
$\left( \mathbb{R}{{\mathbb{H}}^{5}} \right)$. These subgroups are commensurable to discrete hyperbolic reflection groups, and the Vinberg diagrams of the latter are computed.
