1 results
The Explicit Solution of the
-Neumann Problem in a Non-Isotropic Siegel Domain
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 6 / 01 December 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1299-1322
- Print publication:
- 01 December 1997
-
- Article
-
- You have access
- Export citation
-
In this paper, we solve the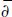
-Neumann problem on (0, q) forms, 0 ≤ q ≤ n, in the strictly pseudoconvex non-isotropic Siegel domain: 
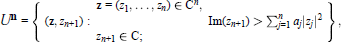where aj > 0 for j = 1,2, . . . , n. The metric we use is invariant under the action of the Heisenberg group on the domain. The fundamental solution of the related differential equation is derived via the Laguerre calculus. We obtain an explicit formula for the kernel of the Neumann operator. We also construct the solution of the corresponding heat equation and the fundamental solution of the Laplacian operator on the Heisenberg group.
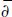-Neumann Problem in a Non-Isotropic Siegel Domain
