We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the self-adjoint second-order scalar difference equation (1) Δ(rnΔxn) +pnXn+1 = 0 and the matrix system (2) Δ(RnΔXn) + PnXn+1 = 0, where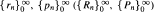 
are seQuences of real numbers (d x d Hermitian matrices) with rn > 0(Rn > 0). The oscillation and nonoscillation criteria for solutions of (1) and (2), obtained in [3, 4, 10], are extended to a much wider class of equations by Riccati and averaging techniques.
