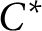 $C^*$
-algebra structure on certain Banach algebra products
$C^*$
-algebra structure on certain Banach algebra products
 $\ast $-SEMISIMPLICITY OF THE
$\ast $-SEMISIMPLICITY OF THE 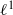 ${\ell }^{1} $-ALGEBRA ON AN ABELIAN
${\ell }^{1} $-ALGEBRA ON AN ABELIAN  $\ast $-SEMIGROUP
$\ast $-SEMIGROUP