In this paper, we study the existence and multiplicity of solutions for Kirchhoff-type superlinear problems involving non-local integro-differential operators. As a particular case, we consider the following Kirchhoff-type fractional Laplace equation:
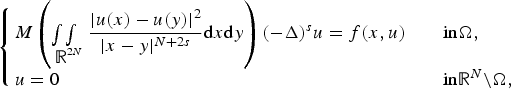 $$\matrix{ {\left\{ {\matrix{ {M\left( {\int\!\!\!\int\limits_{{\open R}^{2N}} {\displaystyle{{ \vert u(x)-u(y) \vert ^2} \over { \vert x-y \vert ^{N + 2s}}}} {\rm d}x{\rm d}y} \right){(-\Delta )}^su = f(x,u)\quad } \hfill & {{\rm in }\Omega ,} \hfill \cr {u = 0\quad } \hfill & {{\rm in }{\open R}^N{\rm \setminus }\Omega {\mkern 1mu} ,} \hfill \cr } } \right.} \hfill \cr } $$
$$\matrix{ {\left\{ {\matrix{ {M\left( {\int\!\!\!\int\limits_{{\open R}^{2N}} {\displaystyle{{ \vert u(x)-u(y) \vert ^2} \over { \vert x-y \vert ^{N + 2s}}}} {\rm d}x{\rm d}y} \right){(-\Delta )}^su = f(x,u)\quad } \hfill & {{\rm in }\Omega ,} \hfill \cr {u = 0\quad } \hfill & {{\rm in }{\open R}^N{\rm \setminus }\Omega {\mkern 1mu} ,} \hfill \cr } } \right.} \hfill \cr } $$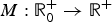 $M:{\open R}_0^ + \to {\open R}^ + $ is a continuous function satisfying certain assumptions, and f(x, u) is superlinear at infinity. By computing the critical groups at zero and at infinity, we obtain the existence of non-trivial solutions for the above problem via Morse theory. To the best of our knowledge, our results are new in the study of Kirchhoff–type Laplacian problems.
$M:{\open R}_0^ + \to {\open R}^ + $ is a continuous function satisfying certain assumptions, and f(x, u) is superlinear at infinity. By computing the critical groups at zero and at infinity, we obtain the existence of non-trivial solutions for the above problem via Morse theory. To the best of our knowledge, our results are new in the study of Kirchhoff–type Laplacian problems.
 2-SYMMETRIC CRITICAL POINT THEOREMS FOR NON-DIFFERENTIABLE FUNCTIONS
2-SYMMETRIC CRITICAL POINT THEOREMS FOR NON-DIFFERENTIABLE FUNCTIONS