A new approach to prove weak convergence of random polytopes on the space of compact convex sets is presented. This is used to show that the profile of the rescaled Schläfli random cone of a random conical tessellation, generated by n independent and uniformly distributed random linear hyperplanes in $\mathbb {R}^{d+1}$ , weakly converges to the typical cell of a stationary and isotropic Poisson hyperplane tessellation in $\mathbb {R}^d$ , as $n\to \infty $ .

Parts of the Brunn–Minkowski theory can be extended to hedgehogs, which are envelopes of families of affine hyperplanes parametrized by their Gauss map. F. Fillastre introduced Fuchsian convex bodies, which are the closed convex sets of Lorentz–Minkowski space that are globally invariant under the action of a Fuchsian group. In this paper, we undertake a study of plane Lorentzian and Fuchsian hedgehogs. In particular, we prove the Fuchsian analogues of classical geometrical inequalities (analogues that are reversed as compared to classical ones).

For positive integers p and q with (p − 2)(q − 2) > 4 there is, in the hyperbolic plane, a group [p, q] generated by reflections in the three sides of a triangle ABC with angles π/p, π/q, π/2. Hyperbolic trigonometry shows that the side AC has length ψ, where cosh ψ = c/s, c = cos π/q, s = sin π/p. For a conformal drawing inside the unit circle with centre A, we may take the sides AB and AC to run straight along radiiwhile BC appears as an arc of a circle orthogonal to the unit circle. The circle containing this arc is found to have radius 1/ sinh ψ = s/z, where z = 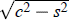, while its centre is at distance 1/ tanh ψ = c/z from A. In the hyperbolic triangle ABC, the altitude from AB to the right-angled vertex C is ζ, where sinh ζ = z.