In 1945–1946, C. L. Siegel proved that an $n$-dimensional lattice $\unicode[STIX]{x1D6EC}$ of determinant $\text{det}(\unicode[STIX]{x1D6EC})$ has at most $m^{n^{2}}$ different sublattices of determinant $m\cdot \text{det}(\unicode[STIX]{x1D6EC})$. In 1997, the exact number of the different sublattices of index $m$ was determined by Baake. We present a systematic treatment for counting the sublattices and derive a formula for the number of the sublattice classes under unimodular equivalence.

Let ${\mathcal{A}}$ be a star-shaped polygon in the plane, with rational vertices, containing the origin. The number of primitive lattice points in the dilate $t{\mathcal{A}}$ is asymptotically $\frac{6}{\unicode[STIX]{x1D70B}^{2}}\text{Area}(t{\mathcal{A}})$ as $t\rightarrow \infty$. We show that the error term is both $\unicode[STIX]{x1D6FA}_{\pm }(t\sqrt{\log \log t})$ and $O(t(\log t)^{2/3}(\log \log t)^{4/3})$. Both bounds extend (to the above class of polygons) known results for the isosceles right triangle, which appear in the literature as bounds for the error term in the summatory function for Euler’s $\unicode[STIX]{x1D719}(n)$.

We solve a randomized version of the following open question: is there a strictly convex, bounded curve 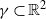$\gamma \subset { \mathbb{R} }^{2} $ such that the number of rational points on 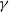$\gamma $, with denominator $n$, approaches infinity with $n$? Although this natural problem appears to be out of reach using current methods, we consider a probabilistic analogue using a spatial Poisson process that simulates the refined rational lattice 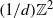$(1/ d){ \mathbb{Z} }^{2} $, which we call 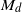${M}_{d} $, for each natural number 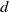$d$. The main result here is that with probability 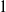$1$ there exists a strictly convex, bounded curve 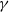$\gamma $ such that 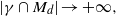$\vert \gamma \cap {M}_{d} \vert \rightarrow + \infty , $ as 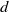$d$ tends to infinity. The methods include the notion of a generalized affine length of a convex curve as defined by F. V. Petrov [Estimates for the number of rational points on convex curves and surfaces. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 344 (2007), 174–189; Engl. transl. J. Math. Sci. 147(6) (2007), 7218–7226].

The similar sublattices of a planar lattice can be classified via its multiplier ring. The latter is the ring of rational integers in the generic case, and an order in an imaginary quadratic field otherwise. Several classes of examples are discussed, with special emphasis on concrete results. In particular, we derive Dirichlet series generating functions for the number of distinct similar sublattices of a given index, and relate them to zeta functions of orders in imaginary quadratic fields.

A necessary and sufficient condition to obtain a volumelike form from an affine connection is given in terms of the Čech cohomology, after the volume-like form is naturally defined without a Riemannian metric. A necessary condition for an affine connection to be a Riemannian connection for some metric is also given.