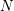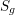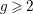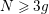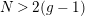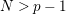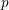In Hirose (Tohoku Math. J. 62 (2010), 45–53), Susumu Hirose showed that, except for a few cases, the order 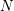$N$ of a cyclic group of self-homeomorphisms of a closed orientable topological surface 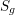$S_{g}$ of genus 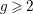$g\geqslant 2$ determines the group up to a topological conjugation, provided that 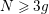$N\geqslant 3g$. Gromadzki et al. undertook in Bagiński et al. (Collect. Math. 67 (2016), 415–429) a more general problem of topological classification of such group actions for 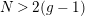$N>2(g-1)$. In Gromadzki and Szepietowski (Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 110 (2016), 303–320), we considered the analogous problem for closed nonorientable surfaces, and in Gromadzki et al. (Pure Appl. Algebra 220 (2016), 465–481) – the problem of classification of cyclic actions generated by an orientation-reversing self-homeomorphism. The present paper, in which we deal with topological classification of actions on bordered surfaces of finite cyclic groups of order 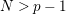$N>p-1$, where 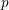$p$ is the algebraic genus of the surface, completes our project of topological classification of ‘‘large” cyclic actions on compact surfaces. We apply obtained results to solve the problem of uniqueness of the actions realizing the solutions of the so-called minimum genus and maximum order problems for bordered surfaces found in Bujalance et al. (Automorphisms Groups of Compact Bordered Klein Surfaces: A Combinatorial Approach, Lecture Notes in Mathematics 1439, Springer, 1990).

Following the analogy between primes and knots, we introduce the refined Milnor invariants for prime numbers and establish their connection with certain Massey products in Galois cohomology. This generalizes the well-known relation between the power residue symbol and cup product and gives a cohomological interpretation of L. Rédei's triple symbol.

Analogues of a theorem of Greenberg about finitely generated subgroups of free groups are proved for quasiconvex subgroups of word hyperbolic groups. It is shown that a quasiconvex subgroup of a word hyperbolic group is a finite index subgroup of only finitely many other subgroups.