Let
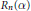 ${{R}_{n}}\left( \alpha \right)$
be the
${{R}_{n}}\left( \alpha \right)$
be the 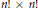 $n!\,\times \,n!$ matrix whose matrix elements
$n!\,\times \,n!$ matrix whose matrix elements
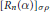 ${{\left[ {{R}_{n}}\left( \alpha \right) \right]}_{\sigma p}}$
, with
${{\left[ {{R}_{n}}\left( \alpha \right) \right]}_{\sigma p}}$
, with  $\sigma$ and
$\sigma$ and  $p$ in the symmetric group
$p$ in the symmetric group
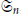 ${{G}_{n}}$
, are
${{G}_{n}}$
, are
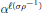 ${{\alpha }^{\ell \left( \sigma {{p}^{-1}} \right)}}$
with
${{\alpha }^{\ell \left( \sigma {{p}^{-1}} \right)}}$
with 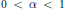 $0\,<\,\alpha \,<\,1$, where
$0\,<\,\alpha \,<\,1$, where 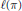 $\ell \left( \text{ }\!\!\pi\!\!\text{ } \right)$ denotes the number of cycles in
$\ell \left( \text{ }\!\!\pi\!\!\text{ } \right)$ denotes the number of cycles in
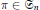 $\text{ }\pi \text{ }\in {{G}_{n}}.$ We give the spectrum of
$\text{ }\pi \text{ }\in {{G}_{n}}.$ We give the spectrum of
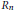 ${{R}_{n}}$
and show that the ratio of the largest eigenvalue
${{R}_{n}}$
and show that the ratio of the largest eigenvalue
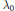 ${{\text{ }\!\!\lambda\!\!\text{ }}_{0}}$
to the second largest one (in absolute value) increases as a positive power of
${{\text{ }\!\!\lambda\!\!\text{ }}_{0}}$
to the second largest one (in absolute value) increases as a positive power of  $n$ as
$n$ as 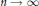 $n\,\to \,\infty$.
$n\,\to \,\infty$.