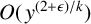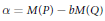Refine search
Actions for selected content:
4 results
IMPROVED LOWER BOUNDS FOR STRONG n-CONJECTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 June 2025, pp. 61-81
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON NEAR-PERFECT NUMBERS OF SPECIAL FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 366-372
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON POWERFUL NUMBERS IN SHORT INTERVALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 99-106
- Print publication:
- August 2023
-
- Article
- Export citation
Every Real Algebraic Integer Is a Difference of Two Mahler Measures
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 2 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-195
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation