Refine search
Actions for selected content:
6 results
An autoregressive growth model for longitudinal item analysis
-
- Journal:
- Psychometrika / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 01 January 2025, pp. 830-850
-
- Article
- Export citation
Exact recovery of Granger causality graphs with unconditional pairwise tests
-
- Journal:
- Network Science / Volume 11 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 06 June 2023, pp. 431-457
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 5 - Models to Disentangle the Between- and Within-subjects Relationship
-
- Book:
- Applied Longitudinal Data Analysis for Medical Science
- Published online:
- 20 April 2023
- Print publication:
- 27 April 2023, pp 76-91
-
- Chapter
- Export citation
Uniformly distributed first-order autoregressive time series models and multiplicative congruential random number generators
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 896-903
- Print publication:
- December 1992
-
- Article
- Export citation
A multiple-threshold AR(1) model
-
- Journal:
- Journal of Applied Probability / Volume 22 / Issue 2 / June 1985
- Published online by Cambridge University Press:
- 14 July 2016, pp. 267-279
- Print publication:
- June 1985
-
- Article
- Export citation
A threshold AR(1) model
-
- Journal:
- Journal of Applied Probability / Volume 21 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 14 July 2016, pp. 270-286
- Print publication:
- June 1984
-
- Article
- Export citation
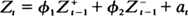 where
where 