1 results
Quasi-isolated blocks and the Alperin–McKay conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 June 2022, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
The Alperin–McKay conjecture is a longstanding open conjecture in the representation theory of finite groups. Späth showed that the Alperin–McKay conjecture holds if the so-called inductive Alperin–McKay (iAM) condition holds for all finite simple groups. In a previous paper, the author has proved that it is enough to verify the inductive condition for quasi-isolated blocks of groups of Lie type. In this paper, we show that the verification of the iAM-condition can be further reduced in many cases to isolated blocks. As a consequence of this, we obtain a proof of the Alperin–McKay conjecture for
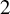$2$
-blocks of finite groups with abelian defect.
