1 results
A posteriori error analysis for parabolicvariational inequalities
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 41 / Issue 3 / May 2007
- Published online by Cambridge University Press:
- 02 August 2007, pp. 485-511
- Print publication:
- May 2007
-
- Article
- Export citation
-
Motivated by the pricing of American options for baskets weconsider a parabolic variational inequality in a boundedpolyhedral domain $\Omega\subset\mathbb{R}^d$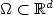
with a continuous piecewisesmooth obstacle. We formulate a fully discrete method by usingpiecewise linear finite elements in space and the backward Eulermethod in time. We define an a posteriori error estimator and showthat it gives an upper bound for the error inL2(0,T;H1 (Ω)). The error estimator is localized in thesense that the size of the elliptic residual is only relevant inthe approximate non-contact region, and the approximability of theobstacle is only relevant in the approximate contact region. Wealso obtain lower bound results for the space error indicators inthe non-contact region, and for the time error estimator.Numerical results for d=1,2 show that the error estimator decayswith the same rate as the actual error when the space meshsize hand the time step τ tend to zero. Also, the error indicatorscapture the correct behavior of the errors in both the contact andthe non-contact regions.
