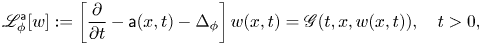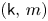1 results
Differential Harnack estimates for a weighted nonlinear parabolic equation under a super Perelman–Ricci flow and implications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this paper, we derive new differential Harnack estimates of Li–Yau type for positive smooth solutions to a class of nonlinear parabolic equations in the form
\[ {\mathscr L}_\phi^{\mathsf a} [w]:= \left[ \frac{\partial}{\partial t} - \mathsf{a}(x,t) - \Delta_\phi \right] w (x,t) = \mathscr G(t, x, w(x,t)), \quad t>0, \]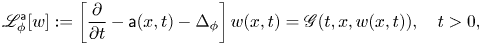on smooth metric measure spaces where the metric and potential are time dependent and evolve under a $({\mathsf k},\, m)$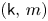
-super Perelman–Ricci flow. A number of consequences, most notably, a parabolic Harnack inequality, a class of Hamilton type global curvature-free estimates and a general Liouville type theorem together with some consequences are established. Some special cases are presented to illustrate the strength of the results.
