We prove some results on weakly almost square Banach spaces and their relatives. On the one hand, we discuss weak almost squareness in the setting of Banach function spaces. More precisely, let 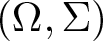 $(\Omega,\Sigma)$ be a measurable space, let E be a Banach lattice and let
$(\Omega,\Sigma)$ be a measurable space, let E be a Banach lattice and let  $\nu:\Sigma \to E^+$ be a non-atomic countably additive measure having relatively norm compact range. Then the space
$\nu:\Sigma \to E^+$ be a non-atomic countably additive measure having relatively norm compact range. Then the space 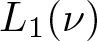 $L_1(\nu)$ is weakly almost square. This result applies to some abstract Cesàro function spaces. Similar arguments show that the Lebesgue–Bochner space
$L_1(\nu)$ is weakly almost square. This result applies to some abstract Cesàro function spaces. Similar arguments show that the Lebesgue–Bochner space 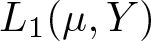 $L_1(\mu,Y)$ is weakly almost square for any Banach space Y and for any non-atomic finite measure µ. On the other hand, we make some progress on the open question of whether there exists a locally almost square Banach space, which fails the diameter two property. In this line, we prove that if X is any Banach space containing a complemented isomorphic copy of c0, then for every
$L_1(\mu,Y)$ is weakly almost square for any Banach space Y and for any non-atomic finite measure µ. On the other hand, we make some progress on the open question of whether there exists a locally almost square Banach space, which fails the diameter two property. In this line, we prove that if X is any Banach space containing a complemented isomorphic copy of c0, then for every 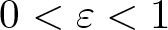 $0 \lt \varepsilon \lt 1$, there exists an equivalent norm
$0 \lt \varepsilon \lt 1$, there exists an equivalent norm  $|\cdot|$ on X satisfying the following: (i) every slice of the unit ball
$|\cdot|$ on X satisfying the following: (i) every slice of the unit ball 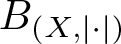 $B_{(X,|\cdot|)}$ has diameter 2; (ii)
$B_{(X,|\cdot|)}$ has diameter 2; (ii) 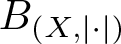 $B_{(X,|\cdot|)}$ contains non-empty relatively weakly open subsets of arbitrarily small diameter and (iii)
$B_{(X,|\cdot|)}$ contains non-empty relatively weakly open subsets of arbitrarily small diameter and (iii) 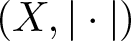 $(X,|\cdot|)$ is (r, s)-SQ for all
$(X,|\cdot|)$ is (r, s)-SQ for all 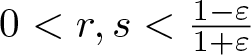 $0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$.
$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$.
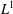 $L^{1}$-SPACES
$L^{1}$-SPACES