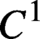1 results
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
-
We obtain a criterion for an analytic subset of a Euclidean space to contain points of differentiability of a typical Lipschitz function: namely, that it cannot be covered by countably many sets, each of which is closed and purely unrectifiable (has a zero-length intersection with every
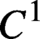$C^1$
curve). Surprisingly, we establish that any set failing this criterion witnesses the opposite extreme of typical behaviour: in any such coverable set, a typical Lipschitz function is everywhere severely non-differentiable.
