Let R be a ring and let 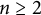 $n\ge 2$. We discuss the question of whether every element in the matrix ring
$n\ge 2$. We discuss the question of whether every element in the matrix ring 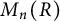 $M_n(R)$ is a product of (additive) commutators
$M_n(R)$ is a product of (additive) commutators 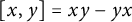 $[x,y]=xy-yx$, for
$[x,y]=xy-yx$, for 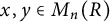 $x,y\in M_n(R)$. An example showing that this does not always hold, even when R is commutative, is provided. If, however, R has Bass stable rank one, then under various additional conditions every element in
$x,y\in M_n(R)$. An example showing that this does not always hold, even when R is commutative, is provided. If, however, R has Bass stable rank one, then under various additional conditions every element in 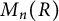 $M_n(R)$ is a product of three commutators. Further, if R is a division ring with infinite center, then every element in
$M_n(R)$ is a product of three commutators. Further, if R is a division ring with infinite center, then every element in 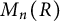 $M_n(R)$ is a product of two commutators. If R is a field and
$M_n(R)$ is a product of two commutators. If R is a field and 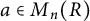 $a\in M_n(R)$, then every element in
$a\in M_n(R)$, then every element in 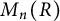 $M_n(R)$ is a sum of elements of the form
$M_n(R)$ is a sum of elements of the form 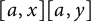 $[a,x][a,y]$ with
$[a,x][a,y]$ with 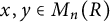 $x,y\in M_n(R)$ if and only if the degree of the minimal polynomial of a is greater than
$x,y\in M_n(R)$ if and only if the degree of the minimal polynomial of a is greater than 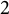 $2$.
$2$.