We give three formulas for meromorphic eigenfunctions (scattering states) of Sutherland's integrable $N$-body Schrödinger operators and their generalizations. The first is an explicit computation of the Etingof-Kirillov traces of intertwining operators, the second an integral representation of hypergeometric type, and the third is a formula of Bethe ansatz type. The last two formulas are degenerations of elliptic formulas obtained previously in connection with the Knizhnik-Zamolodchikov-Bernard equation. The Bethe ansatz formulas in the elliptic case are reviewed and discussed in more detail here: Eigenfunctions are parametrized by a ‘Hermite-Bethe’ variety, a generalization of the spectral variety of the Lamé operator. We also give the $q$-deformed version of our first formula. In the scalar ${\rm sl}_N$ case, this gives common eigenfunctions of the commuting Macdonald-Rujsenaars difference operators.
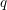 $q$-Boson particle system
$q$-Boson particle system