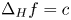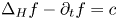1 results
A note on monotonicity and Bochner formulas in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1543-1563
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this note, we prove two monotonicity formulas for solutions of $\Delta _H f = c$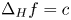
and $\Delta _H f - \partial _t f = c$
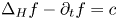in Carnot groups. Such formulas involve the right-invariant carré du champ of a function and they are false for the left-invariant one. The main results, theorems 1.1 and 1.2, display a resemblance with two deep monotonicity formulas respectively due to Alt–Caffarelli–Friedman for the standard Laplacian, and to Caffarelli for the heat equation. In connection with this aspect we ask the question whether an ‘almost monotonicity’ formula be possible. In the last section, we discuss the failure of the nondecreasing monotonicity of an Almgren type functional.
