A modified version of the classical µ-operator as well as the
first value operator and the operator of inverting unary
functions, applied in combination with the composition of
functions and starting from the primitive recursive functions,
generate all arithmetically representable functions. Moreover, the
nesting levels of these operators are closely related to the
stratification of the arithmetical hierarchy. The same is shown
for some further function operators known from computability and complexity
theory.
The close relationships between nesting levels of operators and
the stratification of the hierarchy also hold for suitable
restrictions of the operators with respect to the polynomial
hierarchy if one starts with the polynomial-time computable
functions. It follows that questions around P vs. NP and
NP vs. coNP can equivalently be expressed by closure
properties of function classes under these operators.
The polytime version of the first value operator can be used to
establish hierarchies between certain consecutive levels within
the polynomial hierarchy of functions, which are related to
generalizations of the Boolean hierarchies over the classes
$\mbox{$\Sigma^p_{k}$}$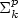 .
.