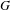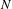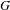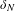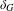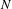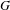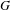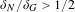Given a group  $G$ and an integer
$G$ and an integer  $n\geq 0$, we consider the family
$n\geq 0$, we consider the family  ${\mathcal F}_n$ of all virtually abelian subgroups of
${\mathcal F}_n$ of all virtually abelian subgroups of  $G$ of
$G$ of  $\textrm{rank}$ at most
$\textrm{rank}$ at most  $n$. In this article, we prove that for each
$n$. In this article, we prove that for each  $n\ge 2$ the Bredon cohomology, with respect to the family
$n\ge 2$ the Bredon cohomology, with respect to the family  ${\mathcal F}_n$, of a free abelian group with
${\mathcal F}_n$, of a free abelian group with  $\textrm{rank}$
$\textrm{rank}$  $k \gt n$ is nontrivial in dimension
$k \gt n$ is nontrivial in dimension  $k+n$; this answers a question of Corob Cook et al. (Homology Homotopy Appl. 19(2) (2017), 83–87, Question 2.7). As an application, we compute the minimal dimension of a classifying space for the family
$k+n$; this answers a question of Corob Cook et al. (Homology Homotopy Appl. 19(2) (2017), 83–87, Question 2.7). As an application, we compute the minimal dimension of a classifying space for the family  ${\mathcal F}_n$ for braid groups, right-angled Artin groups, and graphs of groups whose vertex groups are infinite finitely generated virtually abelian groups, for all
${\mathcal F}_n$ for braid groups, right-angled Artin groups, and graphs of groups whose vertex groups are infinite finitely generated virtually abelian groups, for all  $n\ge 2$. The main tools that we use are the Mayer–Vietoris sequence for Bredon cohomology, Bass–Serre theory, and the Lück–Weiermann construction.
$n\ge 2$. The main tools that we use are the Mayer–Vietoris sequence for Bredon cohomology, Bass–Serre theory, and the Lück–Weiermann construction.