In the present paper we study the number of occurrences of non-overlapping success runs of length 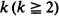 in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.
in a sequence of (not necessarily identical) Bernoulli trials arranged on a circle. An exact formula is given for the probability function, along with some sharp bounds which turn out to be very useful in establishing limiting (Poisson convergence) results. Certain applications to statistical run tests and reliability theory are also discussed.