Search

3 results

Cantor spectrum for CMV and Jacobi matrices with coefficients arising from generalized skew-shifts
Part of
HYUNKYU JUN
Journal:

Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022

Published online by Cambridge University Press:

08 April 2021, pp. 2009-2027

Print publication:

June 2022
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We consider continuous cocycles arising from CMV and Jacobi matrices. Assuming that the Verblunsky and Jacobi coefficients arise from generalized skew-shifts, we prove that uniform hyperbolicity of the associated cocycles is 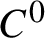$C^0$ -dense. This implies that the associated CMV and Jacobi matrices have a Cantor spectrum for a generic continuous sampling map.

15 - Spectral Properties of Limit-Periodic Operators
- By David Damanik, Jake Fillman
Edited by Matthias Keller, Universität Potsdam, Germany, Daniel Lenz, Universität Potsdam, Germany, Radoslaw K. Wojciechowski
Book:

Analysis and Geometry on Graphs and Manifolds

Published online:

14 August 2020

Print publication:

20 August 2020, pp 382-444
- Chapter
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
Summary

We survey results concerning the spectral properties of limit-periodic operators. The main focus is on discrete one-dimensional Schr\"odinger operators, but other classes of operators, such as Jacobi and CMV matrices, continuum Schr\"odinger operators and multi-dimensional Schrödinger operators, are discussed as well.
We explain that each basic spectral type occurs, and it does so for a dense set of limit-periodic potentials. The spectrum has a strong tendency to be a Cantor set, but there are also cases where the spectrum has no gaps at all. The possible regularity properties of the integrated density of states range from extremely irregular to extremely regular. Additionally, we present background about periodic Schrödinger operators and almost-periodic sequences.
In many cases we outline the proofs of the results we present.

Spectral Properties of Random and Deterministic CMVMatrices
M. Stoiciu
Journal:

Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014

Published online by Cambridge University Press:

17 July 2014, pp. 270-281

Print publication:

2014
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
The CMV matrices are unitary analogues of the discrete one-dimensional Schrödingeroperators. We review spectral properties of a few classes of CMV matrices and describefamilies of random and deterministic CMV matrices which exhibit a transition in thedistribution of their eigenvalues.