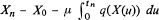1 results
Limit theorems for processes such as the Markov branching process
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 2 / June 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 289-297
- Print publication:
- June 1975
-
- Article
- Export citation
-
Let X(t) be a continuous time Markov process on the integers such that, if σ is a time at which X makes a jump, X(σ)– X(σ–) is distributed independently of X(σ–), and has finite mean μ and variance. Let q(j) denote the residence time parameter for the state j. If tn denotes the time of the nth jump and Xn ≡ X(tb), it is easy to deduce limit theorems for
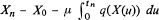from those for sums of independent identically distributed random variables. In this paper, it is shown how, for μ > 0 and for suitable q(·), these theorems can be translated into limit theorems for X(t), by using the continuous mapping theorem.
