We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Arcs of length lk, 0 < lk < 1, k = 1, 2, ···, n, are thrown independently and uniformly on a circumference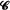 
having unit length. Let P(l1, l2, · ··, ln) be the probability that 
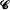is completely covered by the n random arcs. We show that P(l1, l2,· ··, ln) is a Schur-convex function and that it is convex in each argument when the others are held fixed.
