1 results
The structure of finite groups whose elements outside a normal subgroup have prime power orders
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
-
The structure of groups in which every element has prime power order (CP-groups) is extensively studied. We first investigate the properties of group $G$
such that each element of $G\setminus N$
has prime power order. It is proved that $N$
is solvable or every non-solvable chief factor $H/K$
of $G$
satisfying $H\leq N$
is isomorphic to $PSL_2(3^f)$
with $f$
a 2-power. This partially answers the question proposed by Lewis in 2023, asking whether $G\cong M_{10}$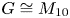
? Furthermore, we prove that if each element $x\in G\backslash N$
has prime power order and ${\bf C}_G(x)$
is maximal in $G$
, then $N$
is solvable. Relying on this, we give the structure of group $G$
with normal subgroup $N$
such that ${\bf C}_G(x)$
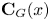is maximal in $G$
for any element $x\in G\setminus N$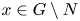
. Finally, we investigate the structure of a normal subgroup $N$
when the centralizer ${\bf C}_G(x)$
is maximal in $G$
for any element $x\in N\setminus {\bf Z}(N)$
, which is a generalization of results of Zhao, Chen, and Guo in 2020, investigating a special case that $N=G$
for our main result. We also provide a new proof for Zhao, Chen, and Guo's results above.
