We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The liner parabolic equation \hbox{$\frac{\pp y}{\pp t}-\frac12\,\D y+F\cdot\na y={\vec{1}}_{\calo_0}u$}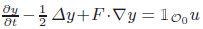
with Neumann boundary condition on a convex open domain 𝒪 ⊂ ℝdwith smooth boundary is exactly null controllable on each finite interval if 𝒪0is an open subset of 𝒪which contains a suitable neighbourhood of the recession cone of \hbox{$\ov\calo$}
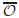. Here, F : ℝd → ℝd is a bounded, C1-continuous function, and F = ∇g, where g is convex and coercive.
