Refine search
Actions for selected content:
6 results
Analysis of Hexagonal Grid Finite Difference Methods for Anisotropic Laplacian Related Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 562-596
- Print publication:
- August 2017
-
- Article
- Export citation
A Compact Scheme for Coupled Stochastic Nonlinear Schrödinger Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 93-125
- Print publication:
- January 2017
-
- Article
- Export citation
A High-Order Numerical Method to Study Three-Dimensional Hydrodynamics in a Natural River
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 23 March 2015, pp. 180-195
- Print publication:
- April 2015
-
- Article
- Export citation
A Fifth-Order Low-Dissipative Conservative Upwind Compact Scheme Using Centered Stencil
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 6 / Issue 6 / December 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 830-848
- Print publication:
- December 2014
-
- Article
- Export citation
A New Approach for Error Reduction in the Volume Penalization Method
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 5 / November 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1181-1200
- Print publication:
- November 2014
-
- Article
- Export citation
Modified Upwinding Compact Scheme for Shock and Shock Boundary Layer Interaction
-
- Journal:
- Communications in Computational Physics / Volume 11 / Issue 3 / March 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1022-1042
- Print publication:
- March 2012
-
- Article
- Export citation
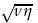 toward the fluid region, where
toward the fluid region, where 