We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we develop a method of solving the Poincaré–Lelong equation, mainly via the study of the large time asymptotics of a global solution to the Hodge–Laplace heat equation on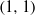 
$(1, 1)$-forms. The method is effective in proving an optimal result when 
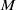$M$ has nonnegative bisectional curvature. It also provides an alternate proof of a recent gap theorem of the first author.
