The game of Cops and Robber is traditionally played on a finite graph. The purpose of this article is to introduce and analyze the game that is played on an arbitrary geodesic space (a compact, path-connected space endowed with intrinsic metric). It is shown that the game played on metric graphs is essentially the same as the discrete game played on abstract graphs and that for every compact geodesic surface there is an integer c such that c cops can win the game against one robber, and c only depends on the genus g of the surface. It is shown that $c=3$ for orientable surfaces of genus $0$ or $1$ and nonorientable surfaces of crosscap number $1$ or $2$ (with any number of boundary components) and that $c=O(g)$ and that $c=\Omega (\sqrt {g})$ when the genus g is larger. The main motivation for discussing this game is to view the cop number (the minimum number of cops needed to catch the robber) as a new geometric invariant describing how complex is the geodesic space.

The game of Cops and Robber is usually played on a graph, where a group of cops attempt to catch a robber moving along the edges of the graph. The cop number of a graph is the minimum number of cops required to win the game. An important conjecture in this area, due to Meyniel, states that the cop number of an n-vertex connected graph is 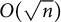$O(\sqrt {n})$. In 2016, Prałat and Wormald showed that this conjecture holds with high probability for random graphs above the connectedness threshold. Moreover, Łuczak and Prałat showed that on a 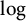$\log $-scale the cop number demonstrates a surprising zigzag behavior in dense regimes of the binomial random graph 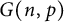$G(n,p)$. In this paper, we consider the game of Cops and Robber on a hypergraph, where the players move along hyperedges instead of edges. We show that with high probability the cop number of the k-uniform binomial random hypergraph 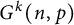$G^k(n,p)$ is 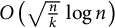$O\left (\sqrt {\frac {n}{k}}\, \log n \right )$ for a broad range of parameters p and k and that on a 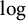$\log $-scale our upper bound on the cop number arises as the minimum of two complementary zigzag curves, as opposed to the case of 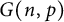$G(n,p)$. Furthermore, we conjecture that the cop number of a connected k-uniform hypergraph on n vertices is 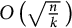$O\left (\sqrt {\frac {n}{k}}\,\right )$.