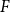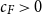A conjecture of Alon, Krivelevich and Sudakov states that, for any graph $F$ , there is a constant $c_F \gt 0$ such that if 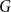$G$ is an 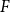$F$ -free graph of maximum degree 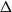$\Delta$ , then 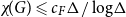$\chi\!(G) \leqslant c_F \Delta/ \log\!\Delta$ . Alon, Krivelevich and Sudakov verified this conjecture for a class of graphs 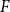$F$ that includes all bipartite graphs. Moreover, it follows from recent work by Davies, Kang, Pirot and Sereni that if 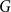$G$ is 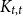$K_{t,t}$ -free, then 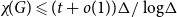$\chi\!(G) \leqslant (t + o(1)) \Delta/ \log\!\Delta$ as 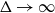$\Delta \to \infty$ . 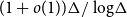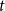We improve this bound to $(1+o(1)) \Delta/\log\!\Delta$ , making the constant factor independent of $t$ . We further extend our result to the DP-colouring setting (also known as correspondence colouring), introduced by Dvořák and Postle.