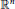For a lattice $L$ of ${{\mathbb{R}}^{n}}$, a sphere 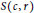$S\left( c,r \right)$ of center $c$ and radius $r$ is called empty if for any 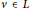$v\,\in \,L$ we have $\parallel v\,-\,c\parallel \,\,\ge \,r$. Then the set 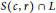$S\left( c,r \right)\,\cap \,L$ is the vertex set of a 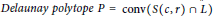$Delaunay\,polytope\,P\,=\,\text{conv}\left( S\left( c,r \right)\cap L \right)$. A Delaunay polytope is called perfect if any affine transformation 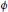$\phi $ such that $\phi \left( P \right)$ is a Delaunay polytope is necessarily an isometry of the space composed with an homothety.

Perfect Delaunay polytopes are remarkable structures that exist only if $n\,=\,1$ or 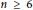$n\,\ge \,6$, and they have shown up recently in covering maxima studies. Here we give a general algorithm for their enumeration that relies on the Erdahl cone. We apply this algorithm in dimension seven, which allows us to find that there are only two perfect Delaunay polytopes: 321, which is a Delaunay polytope in the root lattice 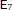${{\text{E}}_{7}}$, and the Erdahl Rybnikov polytope.

We then use this classification in order to get the list of all types of Delaunay simplices in dimension seven and found that there are eleven types.