We characterize Weihrauch reducibility in
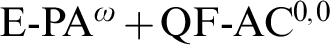 $ \operatorname {\mathrm {E-PA^{\omega }}} + \operatorname {\mathrm {QF-AC^{0,0}}}$
and all systems containing it by the provability in a linear variant of the same calculus using modifications of Gödel’s Dialectica interpretation that incorporate ideas from linear logic, nonstandard arithmetic, higher-order computability, and phase semantics.
$ \operatorname {\mathrm {E-PA^{\omega }}} + \operatorname {\mathrm {QF-AC^{0,0}}}$
and all systems containing it by the provability in a linear variant of the same calculus using modifications of Gödel’s Dialectica interpretation that incorporate ideas from linear logic, nonstandard arithmetic, higher-order computability, and phase semantics.
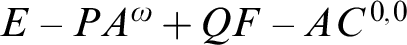 $E-PA^{\omega } + QF-AC^{0,0}$
$E-PA^{\omega } + QF-AC^{0,0}$