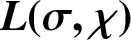 $\boldsymbol{L(\sigma ,\chi )}$
$\boldsymbol{L(\sigma ,\chi )}$
 $L$-FUNCTIONS OVER RATIONAL FUNCTION FIELDS
$L$-FUNCTIONS OVER RATIONAL FUNCTION FIELDS