1 results
An explicit Dobrushin uniqueness region for Gibbs point processes with repulsive interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 March 2022, pp. 541-555
- Print publication:
- June 2022
-
- Article
- Export citation
-
We present a uniqueness result for Gibbs point processes with interactions that come from a non-negative pair potential; in particular, we provide an explicit uniqueness region in terms of activity z and inverse temperature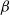
$\beta$
. The technique used relies on applying to the continuous setting the classical Dobrushin criterion. We also present a comparison to the two other uniqueness methods of cluster expansion and disagreement percolation, which can also be applied for this type of interaction.
