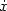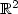The paper is concerned with a class of optimal blocking problems in the plane. We consider a time dependent set R(t) ⊂ ℝ2, described as the reachable set for a differential inclusion. To restrict its growth, a barrier Γ can be constructed, in real time. This is a one-dimensional rectifiable set which blocks the trajectories of the differential inclusion. In this paper we introduce a definition of “regular strategy”, based on a careful classification of blocking arcs. Moreover, we derive local and global necessary conditions for an optimal strategy, which minimizes the total value of the burned region plus the cost of constructing the barrier. We show that a Lagrange multiplier, corresponding to the constraint on the construction speed, can be interpreted as the “instantaneous value of time”. This value, which we compute by two separate formulas, remains constant when free arcs are constructed and is monotone decreasing otherwise.

We consider a class of variationalproblems for differential inclusions, related to thecontrol of wild fires. The area burned by the fire at time t> 0is modelled as the reachable set fora differential inclusion $\dot x$ ∈F(x), starting froman initial set R 0. To block the fire, a barrier can be constructedprogressively in time. For each t> 0, the portion of the wall constructedwithin time t is described by a rectifiable setγ(t) ⊂ $\mathbb{R}^2$ . In this paperwe show that the searchfor blocking strategies and for optimal strategies can be reduced toa problem involving one single admissible rectifiable set Γ⊂ $\mathbb{R}^2$ ,rather than the multifunction t $\mapsto$ γ(t) ⊂ $\mathbb{R}^2$ .Relying on this result, we then developa numerical algorithm for the computation ofoptimal strategies, minimizing the total area burned by the fire.