We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let aπ denote the spectral idempotent of a generalized Drazin invertible element a of a ring. We characterize elements b such that 1 − (bπ − aπ)2 is invertible. We also apply this result in rings with involution to obtain a characterization of the perturbation of EP elements. In Banach algebras we obtain a characterization in terms of matrix representations and derive error bounds for the perturbation of the Drazin Inverse. This work extends recent results for matrices given by the same authors to the setting of rings and Banach algebras. Finally, we characterize generalized Drazin invertible operators A, B ∈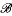 
(X) such that pr(Bπ) = pr(Aπ + S), where pr is the natural homomorphism of 
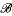(X) onto the Calkin algebra and S ∈
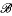(X) is given.
2000 Mathematics subject classification: primary 16A32, 16A28, 15A09.
