This paper considers a bivariate random walk model 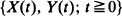 on a rectangular lattice for a particle injected into a fluid flowing in a tank. The numbers of jumps of the particle in the x and y directions in this particular model are correlated. It is shown that when the random walk forms a bivariate Markov chain in continuous time, it is possible to obtain the state probabilities pxy(t) through their Laplace transforms. Two exit rules are considered and results for both of them derived.
on a rectangular lattice for a particle injected into a fluid flowing in a tank. The numbers of jumps of the particle in the x and y directions in this particular model are correlated. It is shown that when the random walk forms a bivariate Markov chain in continuous time, it is possible to obtain the state probabilities pxy(t) through their Laplace transforms. Two exit rules are considered and results for both of them derived.