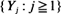Records from are analyzed, where {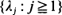Yj} is an independent sequence of random variables. Each Yj has a continuous distribution function Fj = Fλj for some distribution F and some λ j > 0. We study records, record times and related quantities for this sequence. Depending on the sequence of powers , a wide spectrum of behaviour is exhibited.

An autoregressive process ARP(1) with Pareto-distributed inputs, analogous to those of Lawrance and Lewis (1977), (1980), is defined and its properties developed. It is shown that the stationary distributions are Pareto. Further, the maximum and minimum processes are asymptotically Weibull, and the ARP(1) process is shown to be closed under maximization or minimization when the number of terms is geometrically distributed. The ARP(1) process leads naturally to an extremal process in the sense of Lamperti (1964). Statistical inference for the ARP(1) process is developed. An absolutely continuous variant of the Pareto process is described.

A method is reviewed for proving weak convergence in a function-space setting when regular variation is a sufficient condition. Point processes and weak convergence techniques involving continuity arguments play a central role. The method is dimensionless and holds computations to a minimum. Many applications of the methods to processes derived from sums and maxima are given.

Let Xn1 ≦ Xn2 ≦ ··· ≦ Xnn denote the order statistics from a sample of n independent, identically distributed random variables, and suppose that the variables Xnn, Xn, n–1, ···, when suitably normalized, have a non-trivial limiting joint distribution ξ1, ξ2, ···, as n → ∞. It is well known that the limiting distribution must be one of just three types. We provide a canonical representation of the stochastic process {ξn, n ≧ 1} in terms of exponential variables, and use this representation to obtain limit theorems for ξ n as n →∞.

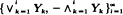We define a vector-valued scheduled maxima sequence M by considering simultaneously the maxima of several i.i.d. sequences, with the number of observations considered from each sequence at any time determined by a random scheduling sequence J. It is shown that the max-min (vector) sequence derived from i.i.d. 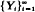can be represented as a mixture of scheduled maxima sequences, giving results for this sequence and the range 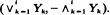A functional limit theorem for the scheduled maxima sequence shows convergence to independent extremal processes. Embedding in a scheduled extremal process gives strong laws, central limit theorems, and laws of the iterated logarithm for the record time of the scheduled maxima sequence, and hence for the max-min sequence and the range.

The maxima of independent Weiner processes spatially normalized with time scales compressed is considered and it is shown that a weak limit process exists. This limit process is stationary, and its one-dimensional distributions are of standard extreme-value type. The method of proof involves showing convergence of related point processes to a limit Poisson point process. The method is extended to handle the maxima of independent Ornstein–Uhlenbeck processes.

The inverse of an extremal process {Y(t), t ≧ 0} is an additive process whose Lévy measure can be computed. This measure controls among other things the Poisson number of jumps of Y while Y is in the vertical window (c, d]. A simple transformation of the inverse of the extremal process governed by Λ (x) = exp{– e–x} is also extremal-Λ (x) and this fact enables one to relate behavior of Y-Λ at t = ∞ to behavior near t = 0. Some extensions of these ideas to sample sequences of maxima of i.i.d. random variables are carried out.

An extremal-F process {Y (t); t ≧ 0} is defined as the continuous time analogue of sample sequences of maxima of i.i.d. r.v.'s distributed like F in the same way that processes with stationary independent increments (s.i.i.) are the continuous time analogue of sample sums of i.i.d. r.v.'s with an infinitely divisible distribution. Extremal-F processes are stochastically continuous Markov jump processes which traverse the interval of concentration of F. Most extremal processes of interest are broad sense equivalent to the largest positive jump of a suitable s.i.i. process and this together with known results from the theory of record values enables one to conclude that the number of jumps of Y (t) in (t1, t2] follows a Poisson distribution with parameter log t2/t1. The time transformation t→ et gives a new jump process whose jumps occur according to a homogeneous Poisson process of rate 1. This fact leads to information about the jump times and the inter-jump times. When F is an extreme value distribution the Y-process has special properties. The most important is that if F(x) = exp {—e–x} then Y(t) has an additive structure. This structure plus non parametric techniques permit a variety of conclusions about the limiting behaviour of Y(t) and its jump times.