We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The paper characterizes matrices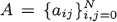 
which have a given system of vectors orthogonal with respect to a given probability distribution as its right eigenvectors. Results of Hoare and Rahman are unified in this context, then all matrices with a given orthogonal polynomial system as right eigenvectors under the constraint a0j = 0 for j ≥ 2 are specified. The only stochastic matrices P = {pij} satisfying p00 + p01 = 1 with the Hahn polynomials as right eigenvectors have the form of the Moran mutation model.
