We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove Lp norm convergence for (appropriate truncations of) the Fourier series arising from the Dirichlet Laplacian eigenfunctions on three types of triangular domains in 
$\mathbb{R}^2$: (i) the 45-90-45 triangle, (ii) the equilateral triangle and (iii) the hemiequilateral triangle (i.e. half an equilateral triangle cut along its height). The limitations of our argument to these three types are discussed in light of Lamé’s Theorem and the image method.
For a family of elliptic operators with periodically oscillating coefficients, 
$-{\rm div}(A(\cdot /\varepsilon )\nabla )$ with tiny ε > 0, we comprehensively study the first-order expansions of eigenvalues and eigenfunctions (eigenspaces) for both the Dirichlet and Neumann problems in bounded, smooth and strictly convex domains (or more general domains of finite type). A new first-order correction term is introduced to derive the expansion of eigenfunctions in L2 or 
$H^1_{\rm loc}$. Our results rely on the recent progress on the homogenization of boundary layer problems.
Suppose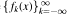 
is a sequence of functions on ℝn with Δfk = fk+1 (where Δ is the Laplacian) that satisfies the growth condition: |fk(x)| ≤ Mk{1 + |x|)a where a ≥ 0 and the constants have sublinear growth 
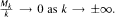Then Δf0 = —f0- This characterizes eigenfunctions f of Δ with polynomial growth in terms of the size of the powers Δkf, —∞ < k < ∞. It also generalizes results of Roe (where a = 0, Mk = M, and n = 1 ) and Strichartz (where a = 0, Mk = M for n). The analogue holds for formally self-adjoint constant coefficient linear partial differential operators on ℝn.
