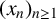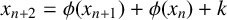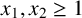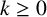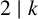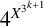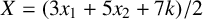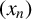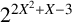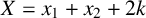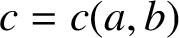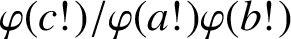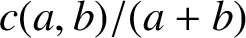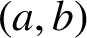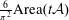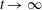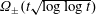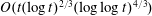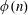Mathematical billiards is much like the real game: a point mass, representing the ball, rolls in a straight line on a (perfectly friction-less) table, striking the sides according to the law of reflection. A billiard trajectory is then completely characterized by the number of elastic collisions. The rules of mathematical billiards may be simple, but the possible behaviours of billiard trajectories are endless. In fact, several fundamental theory questions in mathematics can be recast as billiards problems. A billiard trajectory is called a periodic orbit if the number of distinct collisions in the trajectory is finite. We show that periodic orbits on such billiard tables cannot have an odd number of distinct collisions. We classify all possible equivalence classes of periodic orbits on square and rectangular tables. We also present a connection between the number of different equivalence classes and Euler’s totient function, which for any positive integer N, counts how many positive integers smaller than N share no common divisor with N other than  $1$. We explore how to construct periodic orbits with a prescribed (even) number of distinct collisions and investigate properties of inadmissible (singular) trajectories, which are trajectories that eventually terminate at a vertex (a table corner).
$1$. We explore how to construct periodic orbits with a prescribed (even) number of distinct collisions and investigate properties of inadmissible (singular) trajectories, which are trajectories that eventually terminate at a vertex (a table corner).