We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A finite group is called a CH-group if for every x,y∈G∖Z(G), xy=yx implies that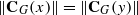 
. Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’, Rend. Sem. Mat. Univ. Padova44 (1970), 97–131] and Rebmann [‘F-Gruppen’, Arch. Math. 22 (1971), 225–230] concerning CA-groups and F-groups, the structure of CH-groups is determined, up to that of CH-groups of prime-power order. Upper bounds are found for the derived length of nilpotent and solvable CH-groups.
