A sequence of finite point processes {Pn} is constructed in 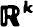 using a Markov sequence of points. Essentially, in the process Pn consisting of n events, the coordinates of these events are simply the first n points of a Markov sequence suitably scaled so that the average density of the process is independent of n. The second-order properties of Pn are discussed and sufficient conditions are found for Pn to converge in distribution to a Poisson process as n →∞. A simple example involving the cardioid distribution is described.
using a Markov sequence of points. Essentially, in the process Pn consisting of n events, the coordinates of these events are simply the first n points of a Markov sequence suitably scaled so that the average density of the process is independent of n. The second-order properties of Pn are discussed and sufficient conditions are found for Pn to converge in distribution to a Poisson process as n →∞. A simple example involving the cardioid distribution is described.

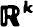 using a Markov sequence of points. Essentially, in the process
using a Markov sequence of points. Essentially, in the process 